I saw a similar-looking fence/railing on an interior balcony once, and for some reason I find it quite soothing.
Here's a pixel art recreation of it for #TilingTuesday (imagine that all the lighter-brown areas are cut out and transparent)

Chunk of the 3d-Penrose Tiling

20.5.4 + sus

after adding 12 rings it seems to become more and more apparent, that the geometric growth of the boundary has a truncated cube as its limit. (3/n) #TilingTuesday

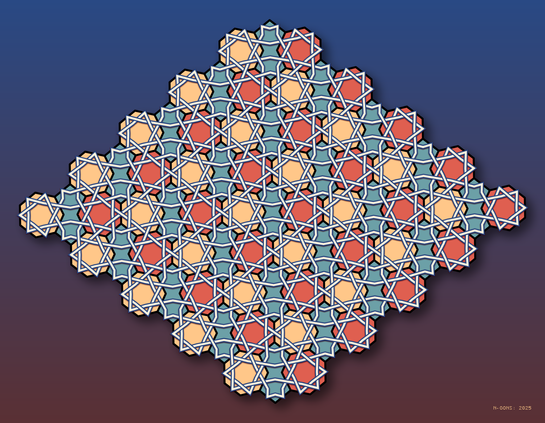
Street paving, Marrakesh, Morocco
#TilingTuesday #Tiling #IslamicPattern #Pattern #Geometry #MathArt #MathsArt #photography

#TilingTuesday
Created in #OneLab

Fragmentarium - 3dickulus Lagrangian mandelbrot J for #tilingtuesday #fractal

#Tiling with #Heptagons for #TilingTuesday

A monohedral heptagonal tiling of an infinite surface, which I suspect to be related to the gyroid, but with different sized necks.
I am going to try to build this one tile by tile, and had forgotten how hard it is to deal with even the simplest of necessities like thickness. So a shout out to people who actually build stuff in the real world. (1/2)
#TilingTuesday

Just because it's #tilingtuesday

Pair of tilings for #TilingTuesday

(...Yes, spot-the-difference edition No knight tiles today, sorry.)

A crystally object for #TilingTuesday

All pentagons are glued to a friend, all triangles face outwards.

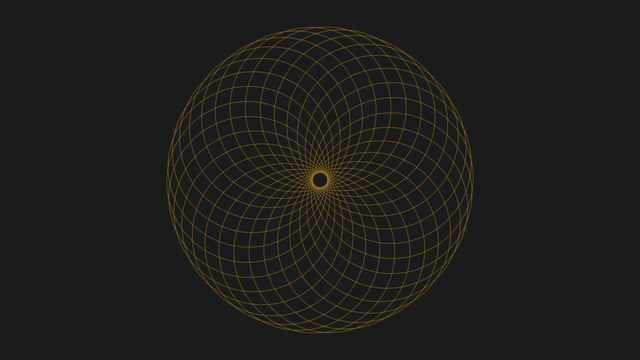
Warping Quasicrystal
From Tetrahedral to Icosahedral.

This looks to me like an echinoderm.
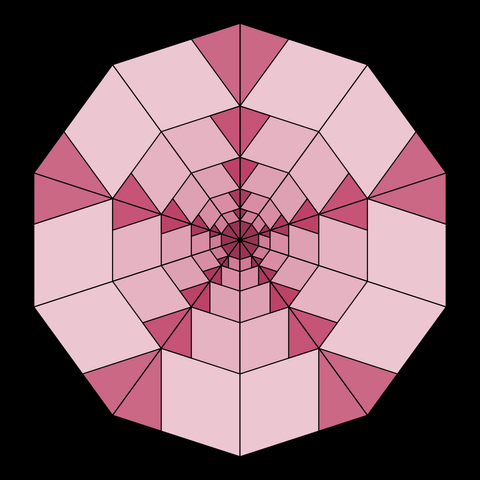
#TilingTuesday #tiling #geometry #mathart #decagon

%
https://idontlikenames.itch.io/apeiroweb
^interactive version sponsored™ by 125bpm姫

Wavy paving, Tokyo, Japan
#tiling #TilingTuesday #pattern #geometry #MathArt #photography

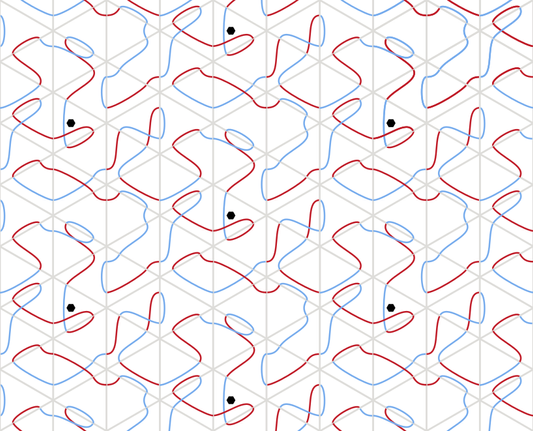
There are 18 ways (up to plane symmetries but not color swapping) to connect two pairs of edges on a triangle tetriamond with curves of different colors. 18 is a good number because it lets us tile a rhombus shaped fundamental domain. (I added the little black hexagons to highlight the underlying pattern of the repeats.

But then the problem is to make meaningful use of the colors, and I failed. It's nice to have all of the segments make one loop. This can't be achieved with alternating segment colors. My next thought was two consecutive segments of one color alternating with two of the other. I couldn't get there though.